פרק רביעי
מבוא לרצפים (א)

תוכן העניינים
הוראות המופיעות בגוף של מבנה while ומתבצעות כל עוד תנאי הלולאה מתקיים צריכות להיות מוזזות ימינה ביחס לשורה הראשונה במבנה. הקוד התקין:
age = input(‘Insert age; -1 to stop: ‘)
while age != ‘-1’:
print(age)
age = input(‘Insert age; -1 to stop: ‘)
(1) מבוא
כל התכניות שדנו בהן בשני הפרקים הקודמים טיפלו בכל ערך – מספר, מחרוזת, ערך בוליאני (True ו-False) – בתור ערך מובחן. גם כשטִפלו בכמה ערכים, הן ראו בכל ערך אובייקט עצמאי ומובחן מערכים אחרים. הביטוי העיקרי לטיפול עצמאי בכל ערך וערך נגע לשמירתם: כל ערך נשמר במשתנה משל עצמו. נחשוב למשל על שמירת מחירי הספרים בתכנית שכתבנו בפרק הראשון:
price1 = float(input(‘Price of book 1: ‘))
price2 = float(input(‘Price of book 2: ‘))
price3 = float(input(‘Price of book 3: ‘))
יש זיקה בין שלושת המספרים שקטע הקוד הזה עוסק בהם: כולם מחירי ספרים. ועם זאת, התכנית קולטת אותם בנפרד זה מזה ושומרת כל אחד במשתנה נפרד. במונחי האנלוגיה של הוראת השמה לכתיבה בלוח שהשתמשנו בה בפרק הראשון, ובהנחה ששלושת המחירים הם 52.1, 73.8 ו-82.4, אפשר לדמות את שמירת המחירים כך:

בפייתון אפשר לטפל בערכים לא במובחן אלה מאלה אלא בתור מכלול אחד, או: בתור אוסף (collection). באנלוגיה ללוח, כך תראה שמירת אוסף של שלושה מחירים:

כאן כל המחירים נשמרים במקום אחד – וספציפית: במשתנה אחד – ומטופלים כמכלול בתור אוסף ערכים.
בפרק זה אנו מתחילים בדיון במגוון סוגים של אוספים בפייתון. כמה מהסוגים הללו, ובהם שניים מהסוגים החשובים ביותר – הסוג מחרוזת והסוג רשימה – משתייכים למשפחה אחת: משפחת הרצפים. מטרתם העיקרית של הפרק הזה ושל הפרק הבא היא לשמש מבוא לעיון ברצפים לסוגיהם. במהלכם נלמד מהו רצף ומה הפעולות השכיחות שפייתון מאפשרת לנו לבצע ברצפים. שני הפרקים, שלא כמו רוב פרקי הספר האחרים, אינם שמים במרכזם דוגמה ספציפית אחת לנתונים או חותרים לכתוב תכנית מסוימת המשתמשת בידע הנלמד. ייעודם הוא לצייד את הקוראות והקוראים ב”ארגז כלים” בסיסי לטיפול ברצפים.
(2) רשימה – טבעה ויצירתה
קודם שנבוא להרחיב את הדיבור בעניין רצפים בכלל, עלינו להקדים ולהתוודע לסוג חשוב של אוספים בפייתון, השייך למשפחת הרצפים. זה הסוג רשימה. שמו בפייתון: list.
תכונה עיקרית של אוסף ערכים מסוג רשימה היא שהערכים הכלולים בו אינם חייבים להיות כולם מסוג אחד. הנה דוגמות לשלושה אוספי ערכים היכולים להרכיב רשימות:
83.2, 75.6, 99.6, 100.0
‘Kolargol’, 5, -7
False, False, False, True, ‘last one’
והנה דוגמה ראשונה לערך מסוג רשימה כפי שהוא נכתב בפייתון:
[‘Kolargol’, 5, -7.3]
שימו לב לסממן ההיכר הצורני של ערך מסוג רשימה: לפנינו אוסף שיש בו ערכים המופרדים זה מזה בפסיקים והתחום משני צדדיו בסוגריים מרובעים.
ככל ערך אפשר להציב במשתנה ערך מסוג רשימה:
lst = [‘Kolargol’, 5, -7.3]
הוראת ההשמה מציבה במשתנה lst את הרשימה המופיעה מצדו הימני של הסימן = .
תנו דעתכם: בתום ביצועה של הוראת ההשמה יש במשתנה lst ערך אחד ולא שלושה! באנלוגיה ללוח:

השמת הרשימה [‘Kolargol’, 5, -7.3] במשתנה lst היא כמו כתיבת ערך אחד בלבד בלוח, ערך מסוג רשימה. אמנם ברשימה זו עצמה יש כמה ערכים; אך היא אינה אלא ערך אחד בלבד.
אפשר ליצור רשימה גם ממשתנים. דוגמה:
item1 = ‘Kolargol’
item2 = 5
item3 = -7.3
lst = [item1, item2, item3]
print(lst)
>>>
[‘Kolargol’, 5, -7.3]
כאן תחמנו שלושה משתנים בסוגריים מרובעים. הרשימה כוללת את הערכים במשתנים אלה. הצבנו אותה במשתנה lst .
גם רשימה יכולה להיות ערך ברשימה. דוגמה:
lst = [‘Kolargol’, 5, -7.3, [‘Here’, ‘I’, ‘am’] ]
כאן הערך הרביעי ברשימה lst הוא עצמו רשימה. ברשימה פנימית זו יש שלושה ערכים.
שיטה שכיחה אחרת ליצירת רשימה היא שימוש בפונקציה list. הפונקציה מקבלת ארגומנט אחד: אובייקט מסוג הנחשב בעיני פייתון לאוסף של ערכים. הפונקציה יוצרת רשימה מהערכים באוסף. כפי שיוסבר להלן מחרוזת היא אוסף של תווים, או, לשם דיוק, אוסף של מחרוזות באורך 1. לכן אם ניתן לפונקציה list ארגומנט שהוא מחרוזת, הפונקציה תחזיר רשימה המורכבת מהתווים במחרוזת. דוגמה:
lst = list(‘together as one’)
print(lst)
>>>
[‘t’, ‘o’, ‘g’, ‘e’, ‘t’, ‘h’, ‘e’, ‘r’, ‘ ‘, ‘a’, ‘s’, ‘ ‘, ‘o’, ‘n’, ‘e’]
בהמשך נדגים את פעולת הפונקציה list על אוספי ערכים מסוגים נוספים.
חוץ מ-list יש הוראות ופונקציות נוספות בפייתון היוצרות רשימה. נדגים כאן אחת נוספת, והיא הפונקציה eval. פונקציה זו משמשת להמרת מחרוזת המציינת רשימה לרשימה.
sLst = input(‘Please enter a list: ‘)
lst = eval(sLst)
print(lst)
>>>
[‘Kolargol’, 5, -7.3]
ההוראה הראשונה מבקשת מהמשתמשת שתכניס רשימה, כלומר מחרוזת הבנויה במבנה של רשימה. לדוגמה המשתמשת יכולה להכניס את רצף התווים הזה:
[‘Kolargol’, 5, -7.3]
לאחר שהקלידה את הסוגר המרובע הסוגר, הקישה המשתמשת במקש ENTER. או אז הוצבה במשתנה sLst המחרוזת הזאת:
“[‘Kolargol’, 5, -7.3]“
ההוראה השנייה בקוד מזמנת את הפונקציה eval ונותנת לה בתור ארגומנט מחרוזת המציינת רשימה. לפי מחרוזת הפונקציה eval יוצרת רשימה ומחזירה אותה. הרשימה המוחזרת מוצבת במשתנה lst ומודפסת.
(3) מחרוזות ורשימות – סוגים של רצפים
מחרוזת ורשימה הם שניהם אוספי ערכים מסוג רצף. רצף (sequence) הוא אוסף של ערכים שמוגדר בו סדר. נעיין למשל באוסף זה:
3, True, ‘goodbye’
הגדרת סדר באוסף זה פירושה שמוגדר מקומו של כל ערך וערך באוסף ביחס לערכים האחרים בו. כך המספר 3 בא לפני כל הערכים האחרים באוסף, הערך הבוליאני True בא אחרי המספר 3 ולפני המחרוזת ‘goodbye’, והערך ‘goodbye’ בא אחרי שני הערכים האחרים באוסף.
לכל אחד מערכים בְרצף יש מספר המציין את מקומו ברצף. נהוג לכנות מספר זה בשם אינדקס (index; בעברית ‘מציין’). האינדקס של המקום הראשון הוא 0 (לא 1!); האינדקס של המקום השני הוא 1. האינדקס של המקום השלישי הוא 2, וכן הלאה. ברצף הדוגמה מוגדרת סדרת האינדקסים 0, 1 ו-2.
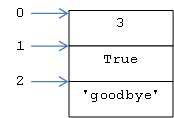
נדגיש: יש להבחין בין הערך ברצף לבין האינדקס של הערך ברצף. האיבר השלישי ברצף המוצג כאן הוא המחרוזת ‘goodbye’ ולא 2; האינדקס 2 מציין את מקומה של המחרוזת ‘goodbye’ ברצף.
נוסף על מערכת האינדקסים 0, 1, 2 וכן הלאה, מתקיימת ברצף גם מערכת אינדקסים נוספת ובה האינדקסים הם שליליים. במערכת זו אין מוגדר אינדקס קטן ביותר (0) אלא אינדקס גדול ביותר: 1-, האינדקס 1- מציין את מקומו של הערך האחרון ברצף. באינדקס 2- מופיע הערך הלפני-אחרון ברצף, וכך לאחור. למשל כך מוגדרת מערכת האינדקסים השליליים ברצף הדוגמה:
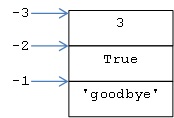
בספר זה נשתמש במערכת האינדקסים החיוביים, אלא אם כן נציין במפורש שקוד נסמך על מערכת האינדקסים השליליים. לפירוט נוסף בנוגע לשימוש במערכת האינדקסים השליליים ראו נספח ג’.
כאמור מחרוזת היא סוג של רצף. טענה זו יכולה להראות מוזרה, כיוון שבמבט ראשון מחרוזת נראית ערך אחד. זאת ועוד: כל התכניות שכתבנו עד כה והשתמשו במחרוזות, טפלו בהן בתור ערך אחד. לדוגמה בפרק הראשון כשמימשנו את ההנחיה “יש לבקש מהמשתמשת להכניס עלות של ספר”, השתמשנו במחרוזת הזאת:
‘Please enter book price: ‘
טיפלנו במחרוזת זו בתור ערך אחד שיש להדפיסו ל-shell (באמצעות הפונקציה input). ועם זאת ניזָכר כי כבר בפרק הראשון, כשהצגנו מחרוזת (string) בתור אחד מסוגי הערכים בפייתון, אמרנו שמחרוזת היא רצף של 0 או יותר תווים. ואמנם מחרוזת היא אוסף ערכים שהוא רצף. נתבונן למשל במחרוזת המוצבת במשתנה s:
s = ‘right left right’
מחרוזת זו היא ערך אחד מסוג מחרוזת. בה בעת מחרוזת זו היא רצף של 16 תווים. כל ערך ברצף הוא מחרוזת באורך 1:
‘r’, ‘i’, ‘g’, ‘h’, ‘t’, ‘ ‘, ‘l’, ‘e’, ‘f’, ‘t’, ‘ ‘, ‘r’, ‘i’, ‘g’, ‘h’, ‘t’
ברצף הערכים הזה מוגדר סדר – התו (כלומר המחרוזת באורך 1) ‘r’ הראשון בא מיד לפני התו ‘i’ הראשון, התו ‘i’ הראשון בא מיד לאחר התו ‘r’ הראשון ומיד לפני התו ‘g’ הראשון, וכן הלאה.
הערך ‘right left right’ הוא אפוא רצף של 16 תווים. האינדקס של המקום הראשון – בו נמצא התו ‘r’ הראשון – הוא 0, האינדקס של המקום השני – בו נמצא התו ‘i’ הראשון – הוא 1, וכן הלאה. אם כן כך רואה פייתון את הערך המוצב במשתנה s:
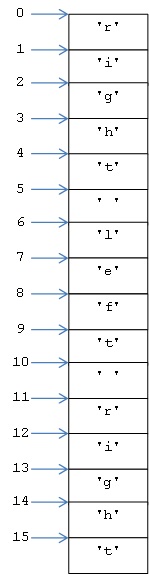
האינדקס המקסימלי המשויך לתו במחרוזת ‘right left right’ הוא 15, אחד פחות ממספר התווים במחרוזת, 16. אין קיים במחרוזת תו באינדקס 16.
כמו בכל רצף גם במחרוזת מוגדרת מערכת אינדקסים שליליים. לדוגמה:
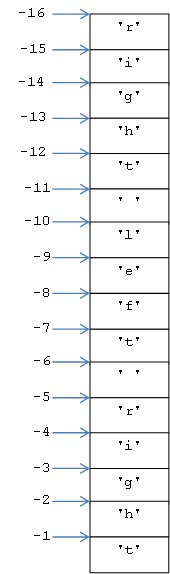
דברים אלה שנאמרו בנוגע לתכונות שיש למחרוזת מתוקף היותה רצף, כלומר הגדרת סדר ומערכת אינדקסים בה, יפים גם בנוגע לרשימה. כך למשל בדבר הרשימה הזאת:
lst = [‘Kolargol’, 5, -7.3, [‘Here’, ‘I’, ‘am’] ]

הרשימה lst היא אוסף סדור של ארבעה ערכים שמוגדרות בו מערכות של אינדקסים. לפי מערכת האינדקסים החיוביים המחרוזת ‘Kolargol’ נמצאת באינדקס 0, המספר 5 נמצא באינדקס 1, המספר 7.3- נמצא באינדקס 2, ובאינדקס 3 יש רשימה פנימית. ברשימה פנימית זו עצמה גם כן מוגדרות מערכות אינדקסים – כך למשל מוגדרת סדרת האינדקסים החיוביים:
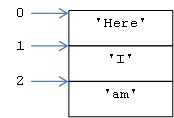
בהמשך פרק זה נראה כיצד אפשר לגשת לערכים בתוך רשימות ובין השאר כיצד ניגשים לערכים בתוך רשימה המוכלת בתוך רשימה. .
(4) אורך של רצף – הפונקציה len
הפונקציה len מקבלת רצף ומחזירה את מספר הערכים בו. דוגמות:
s = ‘nothing new’
length = len(s)
print(length)
>>>
11
lst = [‘one’, 2]
length = len(lst)
print(length)
>>>
2
אורכה של מחרוזת שאין בה תווים הוא 0, וזה גם אורכה של רשימה שאין בה ערכים.
s = “”
length = len(s)
print(length)
>>>
0
lst = []
length = len(lst)
print(length)
>>>
0
רשימה שאין בה ערכים מכונה ‘רשימה ריקה’ (empty list). בדומה מחרוזת שאין בה תווים מכונה ‘מחרוזת ריקה’ (empty string).
(5) יצירת עותק של איבר אחד ברצף – האופרטור [ ]
נפנה עתה לעיין באופרטור נוסף הפועל על רצפים – האופרטור [ ]. הדיון באופרטור חשוב זה נפתח בפרק הנוכחי ויורחב בהמשך הספר. נתחייל ונעיין בשימוש מסוים אחד בו שנתארו כאן לצורך הפשטות כך: יצירת עותק של ערך ברצף (בפרקים הבאים נדייק תיאור זה). התחביר הכללי של שימוש באופרטור [ ] לצורך יצירת עותק של ערך ברצף הוא זה:
sequence[ind]
כאן:
• sequence – שם הרצף
• ind – אינדקס של ערך ברצף שאנו מעוניינים ליצור עותק שלו
דוגמה:
s = ‘abcde’
character = s[3]
print(character)
>>>
d
הפעלת האופרטור [ ] על המחרוזת s באופן זה יוצרת את המחרוזת ‘d’ – התו באינדקס 3 במחרוזת s – ומציבה מחרוזת זאת במשתנה character .
דוגמה נוספת:
lst = [‘first’, ‘second’, ‘third’]
print(lst[1])
>>>
second
באמצעות האופרטור [ ] הקוד ניגש לערך ‘second’ וערך זה מודפס.
אפשר ליצור עותק של רשימה פנימית ברשימה. דוגמה:
lst = [‘Kolargol’, 5, -7.3, [‘Here’, ‘I’, ‘am’] ]
print(lst[3])
>>>
[‘Here’, ‘I’, ‘am’]
כאן יצרנו עותק של הערך המופיע באינדקס 3 ברשימה lst. ערך זה הוא עצמו רשימה.
(6) סריקת רצף – לולאת for
(6.1) עקרונות כלליים
פעולה נוספת ברצפים היא סריקתם: מָעָבַר מְערך לְערך לאורך הרצף, זה אחר זה. סריקת רצף נעשית באמצעות מבנה לולאה שטרם ראינו, ומכונה ‘לולאת for’. לולאת for סורקת ערך אחר ערך ברצף, ועבור כל ערך ברצף מבצעת הוראה או הוראות מסוימות. כיוון שכל רצף הוא בעל גודל נתון, מובן שמספר הסיבובים שמבצעת לולאת for הוא ידוע מראש. היבט זה של פעולתה מבדיל אותה הבדל עקרוני מלולאת while, כפי שראינו בפרק הקודם, לולאת while יכולה להיות מורצת בלי שידוע מראש מספר סיבוביה.
התחביר היסודי של כתיבת לולאת for הוא זה:
for item in sequence:
instruction(s)
כמו מבנה while כך גם מבנה for מורכב משורה ראשונה המַתווה את פעילות הלולאה. לשורה ראשונה זו כמה רכיבים, והם מופיעים בסדר זה:
• המילה השמורה for
• שם משתנה; הוא מכונה ‘משתנה הבקרה’ (control variable)
• האופרטור in
• רצף
• נקודתיים
לולאת for סורקת ערך אחר ערך ברצף sequence. בכל סיבוב של הלולאה הערך הנוכחי מוצב במשתנה הבקרה item, ומבוצעות ההוראות בגוף הלולאה. גוף הלולאה הוא הוראה אחת או הוראות אחדות הבאות לאחר השורה הראשונה במבנה הלולאה. הן מוזזות כמכלול ימינה ביחס לשורה הראשונה.
נדגיש כי שם משתנה הבקרה אינו בהכרח item – אפשר לתת לו שמות אחרים, בתנאי שהם מקיימים את הכללים בקביעת שמות משתנים (ראו פרק ראשון, סעיף 6.2).
הנה דוגמה ראשונה ללולאת for:
seasons = [‘winter’, ‘spring’, ‘summer’, ‘autumn’]
for season in seasons:
print(season)
>>>
winter
spring
summer
autumn
השורה הראשונה בלולאת ה-for קובעת את הרצף הנסרק, איזה ערך ייסרק ראשון, ואיזה ערך ייסרק אחרון. כאן הרצף הנסרק מכיל ארבעה ערכים; הערך הראשון בו הוא ‘winter’, והערך האחרון בו הוא ‘autumn’. מכאן שללולאה יהיו ארבעה סיבובים בדיוק: היא תתחיל בסריקת הערך ‘winter’, והיא תסתיים בסריקת הערך ‘autumn’. בסיבוב הראשון יוצב הערך ‘winter’ במשתנה season וערך זה יודפס. בסיבוב השני יוצב הערך ‘spring’ במשתנה season וערך זה יודפס. בסיבוב השלישי יוצב הערך ‘summer’ במשתנה season וערך זה יודפס. בסיבוב הרביעי והאחרון יוצב הערך ‘autumn’ במשתנה season וערך זה יודפס.
הנה דוגמה לסריקת מחרוזת:
s = “It’s Me!”
for c in s:
print(c)
>>>
I
t
‘
s
M
e
!
דוגמה נוספת:
s = ‘a-zA-Z’
for c in s:
if c != ‘-‘:
print(c)
>>>
a
z
A
Z
chap3כאן הרצף הנסרק מכיל ששה ערכים; הערך הראשון בו הוא ‘a’, והערך האחרון בו הוא ‘Z’. מכאן שללולאה יהיו ששה סיבובים, היא תתחיל בסריקת הערך ‘a’, והיא תסתיים בסריקת הערך ‘Z’. בכל סיבוב יִיבָּחֵן הערך המוצב במשתנה c, והוא יודפס אם הוא שונה מהמחרוזת ‘-‘. בסיבוב הראשון יוצב הערך ‘a’ במשתנה c וערך זה יודפס; בסיבוב השני יוצב הערך ‘-‘ במשתנה c וערך זה לא יודפס; וכן הלאה עד הסיבוב הששי והאחרון, בו יוצב הערך ‘Z’ במשתנה c וערך זה יודפס.
בפרק הקודם (סעיף 9) ראינו כיצד לעקוב אחר פעולתה של לולאת while באמצעות טבלת מעקב. טבלה מעין זו יכולה לשמש גם במעקב אחר לולאת for. הנה כך היא משמשת להבהיר את הנעשה בכל סיבוב וסיבוב של הלולאה המופיעה בקטע הקוד האחרון – כל שורה מתעדת סיבוב אחד.
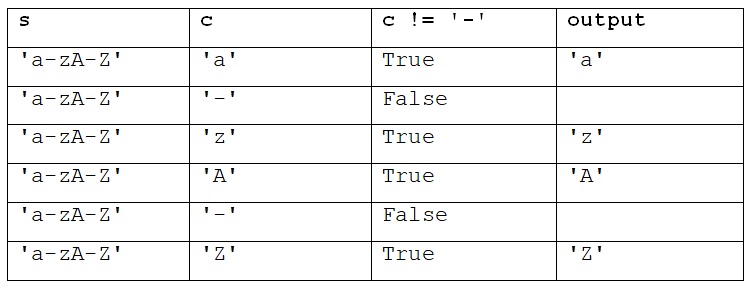
ניתן עתה מבט נוסף בקטע הקוד האחרון:
s = ‘a-zA-Z’
for c in s:
if c != ‘-‘:
print(c)
נשים לב להיבט חשוב של הקוד הזה: הוא יעבוד עבור כל ערך מחרוזת שיוצב במשתנה s, בלי קשר לתווים שהמחרוזת מורכבת מהם ולמספרם. למשל הוא היה פועל באופן תקין עבור המחרוזות ‘begin-end’, ‘no dashes’, ו-“” (מחרוזת ריקה). אמנם הבדלים במחרוזות הנסרקות יכולים לגרום להבדלים בפלט של הקוד. אך החשוב כאן הוא שלולאת ה-for תסרוק את כולן באופן תקין, כאמור ללא קשר להרכבן ולאורכן. כדי להוסיף ולבאר את הדברים, נעיין בבעיה זו:
נתונה רשימה של ציונים (מספרים עשרוניים). שם הרשימה: grades.
יש למצוא את מספר הציונים ברשימה הגדולים מ-80, ולהדפיס מספר זה.
האלגוריתם שנשתמש בו בפתרון הבעיה ערוך בדומה לתבנית המנייה שדנו בה בפרק הקודם (סעיף 3.1). הנה הוא:
(1) הגדרת משתנה בשם grades ואתחולו לרשימה של מספרים עשרוניים (ציונים).
(2) הגדרת משתנה numGrades ואתחולו ל-0
(3) עבור כל ציון grade ברשימה grades
(3.1) אם grade גדול מ-avGrades
(3.1.2) הוספת 1 למספר במשתנה numGrades והצבת התוצאה במשתנה זה
(4) הדפסת המספר במשתנה numGrades
וכך נממש את האלגוריתם:
# 1
grades = ?
# 2
numGrades = 0
# 3
for grade in grades:
# 3.1
if grade > 80:
# 3.1.2
numGrades = numGrades + 1
# 4
print(numGrades)
נשים לב שכאן לא אתחלנו במפורש את הרשימה grades – במקום ערך אתחול מופיע סימן שאלה. כדי שהקוד יפעל באופן תקין הכרחי לאתחל את הרשימה. ועם זאת כאן לא עשינו זאת, והדבר מכוון להדגשה שהקוד יפעל באופן תקין, בלי קשר לתוכן הרשימה grades. כדי להיווכח בכך הריצו את קטע הקוד על מגוון רשימות ציונים תקינות.
נוסיף כמה הערות חשובות בנוגע ללולאת for.
ראשית נדגיש כי כמו בלולאת while גם בלולאת for כל ההוראות בגוף הלולאה מתבצעות בכל סיבוב של הלולאה, אלא אם כן ביצוען מותנה בקיומו של תנאי. נעיין לדוגמה בקוד הזה:
lst = [1, 2, 3]
for item in lst:
print(item * 2)
print(item * 3)
>>>
2
3
4
6
6
9
ללולאה הזאת שלושה סיבובים – אחד עבור כל ערך ברשימה lst. בכל סיבוב מתבצעות (לפי הסדר) שתי ההוראות בגוף הלולאה.
שנית על פי רוב לא ניגש למשתנה הבקרה מחוץ ללולאת for. למשל לא נכתוב קוד זה:
lst = [5, 4, 3, 8]
for item in lst:
print(item)
print(item)
קוד זה לא ייצור שגיאת זמן-ריצה, ובכל זאת נעדיף להימנע ממנו, ולהגביל את מרחק הקיום של משתנה בקרה ללולאה שהוא מוגדר בה בלבד.
שלישית אין הכרח שהפעולות המתבצעות בגוף לולאת for ישתמשו בערכים המוצבים במשתנה הבקרה. מצב זה קורה בדרך כלל כשהמטרה היחידה בשימוש בלולאת for היא הרצת קטע קוד מספר מסוים של פעמים ותו לא. השימוש בלולאת for למטרה זאת ייעשה בדרך כלל באמצעות רצף מסוג range. נציג סוג זה של רצפים ואחר כך נדון בלולאות for המשתמשת בהם.
(6.2) הפונקציה range
בפייתון מוגדר סוג של רצף המכונה range. הוא נוצר באמצעות הפונקציה range. דוגמה:
zeroToFour = range(5)
מתבצע כאן זימון של הפונקציה range. פונקציה זו יוצרת רצף מסוג range. בתור ארגומנט אנו מעבירים אליה מספר שלם חיובי – כאן: 5. מספר זה הוא מספר הערכים שיהיו ברצף. נוסף על כך מספר זה קובע מה יהיו הערכים האלה. הפונקציה range תשים ברצף החדש את כל המספרים השלמים החל מ-0 וכלה במספר השלם הקודם למספר שקיבלה בתור ארגומנט. בדוגמה שלפנינו הרצף החדש יכיל את כל המספרים השלמים החל מ-0 עד 5, ולא כולל 5, כלומר את המספרים 0, 1, 2, 3 ו-4, בסדר זה:
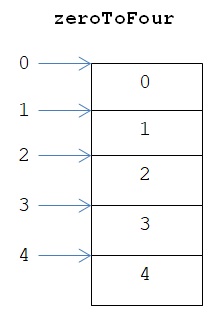
הנה דוגמה נוספת ליצירת רצף של מספרים שלמים באמצעות הפונקציה range. הדוגמה משתמשת בתחביר אחר של זימון range:
oneToSeven = range(1, 8)
כאן העברנו לפונקציה range שני ארגומנטים. הארגומנט הראשון הוא הערך הראשון ברצף הנוצר. כלומר בשימוש בתחביר זה האוסף לא מתחיל ב-0, ובדוגמה שלפנינו הוא מתחיל ב-1. גם כאן ייווצר range המכיל סדרה של מספרים שלמים רצופים. הארגומנט השני קובע מה יהיה המספר האחרון ברצף החדש: המספר הזה הוא מספר שלם אחד לפני המספר שהוא הארגומנט השני. בדוגמה הארגומנט השני הוא 8, ולכן הסדרה תכיל את כל המספרים השלמים בין 1 (כולל) ל-8 (לא כולל).
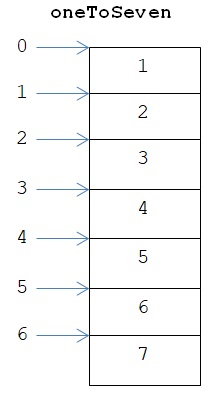
ניתן דעתנו עכשיו לזימון של הפונקציה range בקטע קוד זה:
seasons = [‘winter’, ‘spring’, ‘summer’, ‘autumn’]
range(len(seasons))
מה הרצף שמחזירה הפונקציה range בזימונה זה? הארגומנט המועבר אליה הוא ערך ההחזרה של הפעלת הפונקציה len על הרשימה seasons, כלומר 4. מכאן שערך ההחזרה של הפונקציה range הוא הסדרה הזאת:
0, 1, 2, 3
עיינו בסדרה זו. יש זיקה מסוימת בינה ובין הרשימה seasons: זו סדרת האינדקסים המוגדרת ברשימה. עתה עיינו בקטע הקוד הזה:
s = ‘Ta da!’
range(len(s))
כאן הפונקציה range מקבלת מהפונקציה len את המספר 6 – אורך המחרוזת s – ומשתמשת בו בתור ארגומנט כדי ליצור את הסדרה הזאת:
0, 1, 2, 3, 4, 5
וזו אינה אלא סדרת האינדקסים המוגדרת במחרוזת s. הלקח הכללי העולה מכאן הוא שאם נרצה לקבל את סדרת האינדקסים של רצף seq נוכל להרכיב את הפונקציה len והפונקציה range כך:
range(len(seq))
כפי שנראה להלן, ליצירת סדרת אינדקסים של רצף באופן זה יש חשיבות בסריקת אינדקסים של רצף.
נעיר לסיום כי הסדרה שיוצרת range היא רצף “חלש” יותר מהרצפים העיקריים המוגדרים בפייתון, ובייחוד מרשימה. אמנם אפשר להפעיל על סדרה כזו פעולות מסוימות המופעלות על רשימות, כגון הפונקציה len והאופרטור [ ]. אך אלו היוצאות מן הכלל שאינן מעידות עליו. פעמים רבות, כשנרצה לטפל בסדרה שמפיקה הפונקציה range בדומה לטיפול ברשימה, נקדים ונמיר אותה לרשימה באמצעות הפונקציה list. הנה דוגמה להמרה כזו:
lst = list(range(2, 5))
print(lst)
>>>
[2, 3, 4]
בזכות ההמרה כאן נוכל לטפל בסדרה שהפיק זימון ה-range בתור רשימה.
(6.3) לולאת for לביצוע קטע קוד מספר פעמים ידוע מראש
נעיין בבעיה זו:
יש להדפיס 10 פעמים את המחרוזת ‘!Jump’.
פתרון הבעיה תובע ביצוע פעולה מסוימת מספר מוגדר של פעמים. בפייתון הפתרון המקובל לבעיה מסוג זה הוא שימוש בלולאת for באמצעות רצף שיוצרת הפונקציה range. הנה מימוש של פתרון:
for i in range(10):
print(‘Jump!’)
לשורה הראשונה של הלולאה יש כאן ייעוד מוגדר אחד ויחיד: לגרום להוראה בגוף הלולאה לרוץ מספר מסוים של פעמים (10). הייעוד הזה מושג באמצעות יצירת range שיש בו עשרה ערכים, וסריקת ה-range הזה. הערכים ב-range הם 0 עד 9, אך אין לכך כל חשיבות כיוון שלא נעשה בהם שימוש בגוף הלולאה. אפשר היה לכתוב גם כך:
for i in range(7, 17):
print(‘Jump!’)
וגם זה קוד שיכול לפתור את הבעיה, כיוון שגם בו יש ללולאה עשרה סיבובים.
בפרק השלישי (סעיף 8) ראינו שאפשר להשתמש גם בלולאת while כדי לבצע סדרת הוראות מספר מוגדר של פעמים. הנה אחת הדוגמות שראינו לשימוש בלולאת while למטרה זו:
sumGrades = 0
gradesNum = 5
i = 1
while i <= gradesNum:
grade = input(‘Please enter grades: ‘)
sumGrades = sumGrades + float(grade)
i = i + 1
print(‘Average grade is ‘, sumGrades / gradesNum)
קטע קוד זה קולט 5 ציונים – לשם דיוק: הוא קולט ציונים שמספרם מוצב במשתנה gradesNum – מחשב את ממוצעם ומדפיס אותו. כפי שהסברנו בדיון בקטע זה בפרק השלישי, בפייתון נעדיף לממשו באמצעות בלולאת for, למשל כך:
gradesNum = 5
sumGrades = 0
for i in range(gradesNum):
grade = input(‘Please enter grades: ‘)
sumGrades = sumGrades + float(grade)
print(‘Average grade is ‘, sumGrades / gradesNum)
השורה הראשונה בקוד הזה קובעת שיש ללולאה 5 סיבובים בדיוק. שלא כמו בשימוש בלולאת while, קביעה זו לא דרשה אתחול מפורש של משתנה הבקרה i ל-0, והוספת 1 למספר המוצב בו בכל סיבוב של הלולאה. בה בעת כמו קטע הקוד המשתמש בלולאת while, גם קטע הקוד הזה יוכל לשמש אותנו אם נרצה לקלוט מספר אחר של ציונים: כל שיהיה עלינו לעשות הוא לשנות את המספר המוצב במשתנה gradesNum.
(6.4) סריקת אינדקסים
בכל הדוגמות ללולאת for שהובאו עד כה סרקנו ערכים המופיעים ברצפים. כך למשל בדוגמה הראשונה שדנו בה:
seasons = [‘winter’, ‘spring’, ‘summer’, ‘autumn’]
for season in seasons:
print(season)
הסריקה המתבצעת בלולאה מתחילה בערך ‘winter’, ממשיכה לערך ‘spring’, עוברת לערך ‘summer’, ומסתיימת בערך ‘autumn’. כל ערך מוצב בתורו במשתנה season.
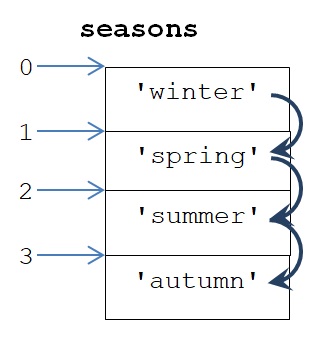
לעתים נכתוב לולאות הסורקות את האינדקסים שהערכים ברצף נמצאים בהם. למשל בדוגמה כאן במקום לסרוק את הערכים ברשימה, היינו יכולים לסרוק את האינדקסים שלהם – 0, 1, 2 ו-3 – ולהציב כל אחד מהם בתורו במשתנה הבקרה של הלולאה.
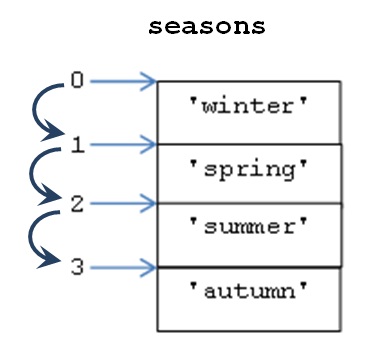
כיצד נסרוק את האינדקסים ברשימה seasons, וככלל ברצף? דרך אחת היא ליצור רצף של האינדקסים הללו באמצעות הפונקציה range ולהפעיל על רצף זה את לולאת for, כך:
seasons = [‘winter’, ‘spring’, ‘summer’, ‘autumn’]
for ind in range(len(seasons)):
print(seasons[ind])
>>>
winter
spring
summer
autumn
הזימון של הפונקציה range על אורך הרשימה seasons – כלומר על 4 – יצר את סדרת האינדקסים של הרשימה – 0 עד 3. לולאת ה-for סרקה את המספרים בסדרה הזאת והשתמשה בהם כדי לגשת לכל המחרוזות ברשימה ולהדפיסן. שיטה זו לסריקת המחרוזות ברשימה seasons ולהדפסתן היא מסורבלת ומורכבת יותר מסריקת ישירה של המחרוזות ברשימה כך:
seasons = [‘winter’, ‘spring’, ‘summer’, ‘autumn’]
for season in seasons:
print(season)
ואם כן עולה השאלה, מדוע נרצה לסרוק אינדקסים של ערכים ברצף ולא לסרוק את הערכים עצמם? התשובה היא שלעתים בגוף הלולאה אנו זקוקים לשמור את האינדקס שבו מופיע הערך הנסרק הנוכחי ולא את הערך עצמו. נעיין למשל בבעיה זו:
נתונה רשימה של מספרים שלמים lst. ברשימה יש לפחות שני מספרים.
יש לבדוק אם יש ברשימה lst מספר הקטן מהמספר העוקב לו ברשימה.
אם יש מספר כזה, התכנית תדפיס False, ואם אין – היא תדפיס True.
למשל אם זו הרשימה lst
lst = [4, 2, 3, 3]
התכנית צריכה לבדוק אחד-אחד את הזוגות 4 ו-2, 2 ו-3, 3 ו-3, ולבדוק: אם 4 קטן מ-2, אם 2 קטן מ-3, ואם 3 קטן מ-3. בבדיקת הזוג 2 ו-3 התכנית תמצא ש-2 קטן מ-3 ולכן תדפיס True.
נכתוב את התכנית לפי אלגוריתם זה:
(1) נגדיר משתנה found ונציב בו False
(2) נסרוק את האינדקסים המוגדרים ברשימה lst
החל מ-0 ועד האינדקס של הערך הלפני אחרון ברשימה;
נציב את האינדקס הנסרק הנוכחי במשתנה i, ועבור כל אינדקס i
(2.1) אם הערך באינדקס i זהה לערך באינדקס i+1
(2.2) נציב את הערך True במשתנה found
(3) נדפיס את found
בצעד 1 אנו מאתחלים את המשתנה found לערך הבוליאני False. אם התכנית תמצא זוג מספרים סמוכים המקיים את הנדרש, המשתנה found יכיל את הערך True בסוף ביצוע האלגוריתם. סריקת הזוגות נסמכת על סריקת האינדקסים המוגדרים ברשימה lst, לא כולל האינדקס של הערך האחרון. למשל אם זו הרשימה lst:
lst = [1, 2, 3, 3]
נסרקים האינדקסים האלה:
0, 1, 2
ומתבצעות בדיקות של הזוגות האלה: זוג המספרים באינדקסים 0 ו-1, זוג המספרים באינדקסים 1 ו-2, וזוג המספרים באינדקסים 2 ו-3.
הנה מימוש של האלגוריתם:
# 1
found = False
# 2
for i in range(len(lst) – 1):
# 2.1
if lst[i] < lst[i + 1]:
# 2.1.1
found = True
# 3
print(found)
שני צדדים של המימוש הזה ראויים לתשובת לב. ראשית תנו דעתכם להוראה היוצרת את סדרת האינדקסים הנסרקים:
range(len(lst) – 1)
כיוון שמועבר לפונקציה range אורך הרשימה פחות 1, סדרת האינדקסים לא תכיל את האינדקס של הערך האחרון ברשימה (נזכיר כי לפי הגדרת הבעיה, הרשימה lst מכילה לפחות שני מספרים).
עניין חשוב אחר נוגע ללב התכנית – פעולת ההשוואה בצעד 2.1. הפעולה הזאת תובעת גישה לערך ברשימה העוקב לערך המופיע באינדקס הנסרק הנוכחי i, כלומר לערך באינדקס i+1. היא מתאפשרת כיוון שאנו סורקים כאן אינדקסים ברשימה ולא ערכים ברשימה.
נעיין בבעיה נוספת. נתונות שתי רשימות שוות גודל, lst1 ו-lst2. אין ידוע בדיוק מה הערכים שיש ברשימות, אך נתון שיש בהן זוג אחד בלבד של ערכים מקבילים (כלומר ערכים הנמצאים באינדקס שווה) שהם זהים. עלינו לכתוב תכנית המוצאת את האינדקס שבו נמצאים הערכים המקבילים הזהים. לדוגמה נניח שאלו שתי הרשימות הנתונות:
lst1 = [5, 3, 3, 8]
lst2 = [6, 5, 3, 6]
lst1 ו-lst2 שתיהן רשימות באורך 4. יש בהן זוג אחד של ערכים הנמצאים באינדקס זהה ושווים זה לזה: שניהם המספר 3. התכנית צריכה למצוא את האינדקס ששני המספרים נמצאים בו. גם האלגוריתם שישמש בפתרון הבעיה הזאת יבוסס על סריקת אינדקסים, וספציפית על סריקת אינדקסים מקבילים בשתי הרשימות. בדוגמה שלפנינו האינדקסים הם אלה (זכרו ששתי הרשימות בגודל שווה):
0, 1, 2, 3
והאלגוריתם הוא זה:
(1) עבור כל אינדקס i בסדרת האינדקסים המוגדרת בשתי הרשימות
(1.1) אם הערך באינדקס i ברשימה lst1 זהה לערך באינדקס i ברשימה lst2
(1.1.1) נשמור את האינדקס i במשתנה pairInd
(2) נדפיס את pairInd
כדי ליצור את סדרת האינדקסים הנסרקת בצעד 1, נזמן את הפונקציה range ונעביר אליה ארגומנט אחד: אורך הרשימות (שתיהן באורך שווה ולכן אפשר לתת את אורך lst1 או אורך lst2). כך נראה הזימון:
range(len(lst1))
הפונקציה range מקבלת כאן ארגומנט אחד: גודל הרשימה lst1. בדוגמה הגודל הזה הוא 4. לכן ה-range שהפונקציה range תחזיר הוא זה:
0, 1, 2, 3
וזו בדיוק סדרת האינדקסים ברשימות הדוגמה הנבדקות.
אם כן כך ייראה מימוש האלגוריתם:
# 1
for i in range(len(lst1)):
# 1.1
if lst1[i] == lst2[i]:
# 1.1.1
pairInd = i
# 2
print(pairInd)
נעיר כי פעמים רבות בסריקת אינדקסים של רצף נעדיף להשתמש בפונקציה enumerate ולא בשילוב של לולאת for והפונקציה range שהוצג כאן. נרחיב את הדיבור בעניין זה כשנדון ברשומות בפרק השמיני. כמו כן אם עלינו לסרוק ערכים מקבילים בשני רצפים או יותר לשם יצירת רצפים מהערכים המקבילים, וליצור רצף אחד מהערכים האלה עצמם, נוכל לעשות זאת באמצעות פונקציה ייעודית. לעניין זה ראו נספח ז’.
(6.5) קטיעת לולאת for
בפרק הקודם ראינו כיצד להשתמש בהוראות break ו-continue כדי לקטוע לולאת while. אפשר להשתמש בשתי הוראות אלו גם בלולאת for, ולמטרות שווות. נעיין בבעיה דומה לבעיה שעסקנו בה בסוף הסעיף הקודם: נתונות שתי רשימות שוות גודל, lst1 ו-lst2. אין ידוע בדיוק מה הערכים שיש ברשימות, אך נתון שיש בהן לפחות זוג אחד של ערכים מקבילים – כלומר ערכים הנמצאים באינדקס שווה – שהם זהים. יש למצוא את האינדקס שמופיע בו הראשון מזוגות אלו. למשל נניח שהרשימות הן אלו:
lst1 = [5, 3, 3, 5]
lst2 = [6, 3, 5, 5]
ברשימות אלו יש שני זוגות של ערכים מקבילים שווים: זוג אחד באינדקס 1, וזוג שני באינדקס 3. התכנית צריכה להחזיר את האינדקס 1.
זו התכנית שהצענו בתור פתרון לבעיה שהוצגה בסעיף הקודם, ולפיה יש רק זוג אחד של ערכים מקבילים שווים:
for i in range(len(lst1)):
if lst1[i] == lst2[i]:
pairInd = i
תכנית זו אינה מתאימה לשמש פתרון לבעיה שלפנינו כאן, ובייחוד במצב שיש בשתי הרשימות יותר מזוג אחד של ערכים מקבילים שווים. הרי אם היא תמצא זוג ראשון של ערכים מקבילים שווים בשתי הרשימות, היא לא תפסיק את סריקת האינדקסים; ותמשיך ותחפש זוגות נוספות, ועבור כל זוג כזה תציב במשתנה pairInd את האינדקס שהזוג נמצא בו. בסופה יוצב ב-pairInd האינדקס שבו מופיע הזוג האחרון של ערכים מקבילים שווים. למשל עבור הרשימות האלו:
lst1 = [5, 3, 3, 5]
lst2 = [6, 3, 5, 5]
בסוף התכנית יוצב במשתנה pairInd האינדקס 3 ולא האינדקס 1, כפי שנדרש.
באמצעות ההוראה continue נוכל לשכתב את התכנית כדי שתתאים לבעיה שאנו עוסקים בה כאן. הנה השכתוב:
pairInd = -1
for i in range(len(lst1)):
if pairInd != -1:
continue
if lst1[i] == lst2[i]:
pairInd = i
התכנית מתחילה באתחול המשתנה pairInd – היא מציבה בו את המספר 1- . בתחילת הלולאה, לפני הבדיקה אם באינדקס הנוכחי i מופיע זוג ערכים מקבילים שווים, מתבצעת בדיקה אחרת: האם כבר נמצא זוג כזה? ברור כי אם אמנם כבר נמצא, pairInd כבר אינו מכיל 1- (שימו לב שמשתנה הבקרה i מכיל אינדקסים חיוביים בלבד). אם אלה הם פני הדברים, מבוצעת ההוראה continue, וערכו של המשתנה pairInd לא ישתנה גם אם יימצאו זוגות נוספים של ערכים מקבילים שווים. למשל עבור הרשימות האלו:
lst1 = [5, 3, 3, 5]
lst2 = [6, 3, 5, 5]
בסוף התכנית יוצב במשתנה pairInd האינדקס 1.
נניח עכשיו כי הרשימות lst1 ו-lst2 הן ארוכות: למשל בכל אחת משתי הרשימות יש טריליון (1000000000000) מספרים. נניח בנוסף כי הזוג הראשון של ערכים מקבילים שווים נמצא באינדקס 0. במצב עניינים זה התכנית מבצעת טריליון פחות אחד סיבובים מיותרים של גוף הלולאה: אין צורך בהם כיוון שכבר בסיבוב הראשון נמצא זוג ערכים מקבילים שווים, והתכנית צריכה לחחזיר את האינדקס של הזוג הזה. דרך אחת לפתור את הבעיה היא באמצעות שימוש בהוראה break במקום ההוראה continue, כך:
pairInd = -1
for i in range(len(lst1)):
if lst1[i] == lst2[i]:
pairInd = i
if pairInd != -1:
break
print(pairInd)
כאן, ברגע שמתברר כי אותר הזוג הראשון של ערכים מקבילים שווים, נשמר האינדקס שהם נמצאים בו, זרימת הלולאה נפסקת, וזרימת התכנית כולה ממשיכה להוראה הבאה לאחר הלולאה – כאן הובאה בתור דוגמה הוראת הדפסה של האינדקס שאותר.
(6.6) תבניות בסריקת רצפים - התניה לפי סוג ערך
בדיון בלולאת while בחנו תבניות השכיחות בכתיבת לולאות מסוג זה: תבניות למניית ערכים, לחישוב סכום, למציאת ערך מקסימלי ולמציאת ערך מינימלי. אפשר להשתמש בתבניות כאלה גם בסריקת רצפים באמצעות לולאת for. ואולם כפי שנראה בפרק הבא בפייתון עומדות לרשותנו פונקציות המייתרות את השימוש בלולאת for בהקשרים כאלה, ומשיגות את המבוקש אגב קיצור הקוד. בכל זאת יש תבניות החוזרות על עצמן גם בכתיבת אלגוריתמים ותכניות לפתרון בעיות הדורשות סריקת רצפים בלולאת for. נעיין כאן באחת מהן: תבנית לבדיקת סוגי הערכים הנסרקים.
כפי שראינו רשימה היא אוסף שיכול להכיל ערכים מסוגים מגוונים. במקרים רבים נרצה לסרוק רשימה ולהפעיל פעולות מסוימות רק על ערכים מסוגים מסוימים בה. אפשר לבסס אלגוריתמים הפותרים בעיות כאלו על תבנית זו:
(1) עבור כל ערך ברשימה
(1.1) אם הערך הנסרק הנוכחי הוא מסוג מסוים
(1.1.1) נבצע פעולה מתאימה
עיינו למשל בבעיה הזאת:
נתונה רשימה של הכנסות משקי בית בשנה. הרשימה באורך כלשהו.
כל ערך ברשימה הוא גובה הכנסה מוערך (בעשרות אלפי שקלים),
או המחרוזת ‘NA’ אם לא ידוע גובה ההכנסה. לדוגמה:
incomes = [83, ‘NA’, 78, 99, ‘NA’]
יש למצוא את סכום הכנסות משקי הבית ברשימה, ולהדפיס סכום זה.
הנה תכנית הפותרת את הבעיה:
sumIncomes = 0
for income in incomes:
if type(income) == int:
sumIncomes = sumIncomes + income
print(sumIncomes)
לאחר אתחול משתנה-סכום ל-0, הקוד סורק ערער-ערך ברשימה incomes ומוסיף לסכום ההכנסות אך ורק ערכים שהם מספרים שלמים (כלומר הכנסות ולא המחרוזת ‘NA’). הבדיקה אם הערך הנוכחי הוא מספר שלם מתבצעת באמצעות הפונקציה type. כפי שראינו בפרק הראשון (סעיף 7.4), פונקציה זו מקבלת ערך ומחזירה את שם הסוג שלו (עד כה הכרנו את שמות הסוגים int, str, float, list ו-range). לצורך הבדיקה אפשר להשתמש גם בפונקציה אחרת: isinstance. פונקציה זו מקבלת ערך ושם של סוג, בסדר זה. היא מחזירה True אם הערך הוא מהסוג ששמו ניתן לה, או False אם הערך אינו מהסוג ששמו ניתן לה. הנה גרסה נוספת של התכנית, גרסה המשתמשת בפונקציה isinstance:
sumIncomes = 0
for income in incomes:
if isinstance(income, int):
sumIncomes = sumIncomes + income
print(sumIncomes)
אם הערך הנסרק הנוכחי הוא מסוג int, הפונקציה isinstance תחזיר את הערך True, וההכנסה הנסרקת הנוכחית תיתוסף לסכום ההולך ומצטבר.
(7) סיכום
בפרק זה ערכנו היכרות ראשונה עם רצפים, והתוודענו לכמה פעולות חשובות שאפשר לבצע בהם. בסיכום הפרק ראוי לנסח במפורש ולהדגיש כמה נקודות שעלו בו במשתמע. ראשית ראינו כי מספר הסיבובים של לולאת for הוא ידוע מראש. מאפיין זה של לולאת for מבדיל אותה מלולאת while, שמספר הסיבובים שלה אינו בהכרח ידוע מראש. הבדל חשוב נוסף בין שני סוגי הלולאות קשור בכך שלולאת for, שלא כמו לולאת while, נמנית עם משפחת הפעולות שנועדו לטיפול ברצפים. נקודה אחרת נוגעת להשוואה בין רצפים, וככלל – בין אוספים. הפרק הנוכחי וכמוהו גם הפרק הבא מדגישים את המשותף לרצפים. אך מעצם קיומם של כמה סוגי רצפים ברור כי יש הבדלים ביניהם (שאם לא כן, היינו יכולים להסתפק בסוג אחד בלבד). כמה הבדלים כאלה כבר התבררו מן הנאמר בפרק זה. כך למשל רצף שהוא מחרוזת, שלא כמו רצף מסוג רשימה, יכול להכיל אך ורק ערכים מסוג אחד: תווים. בפרקים הבאים נפרט את הקווים המייחדים רשימות, מחרוזות, וסוגים אחרים של אוספים, בהם גם אוספים שאינם רצפים.